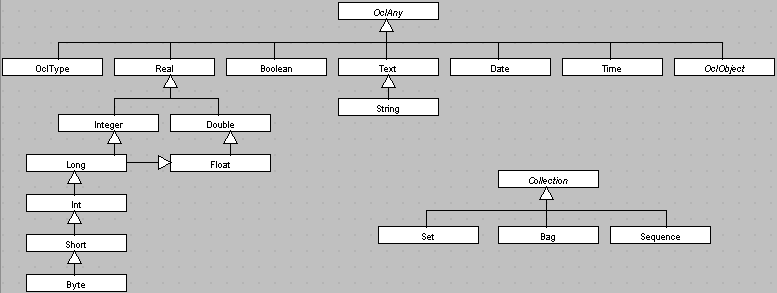
A typed programming language must defined basic types. Xion basic types are predefined classes which do not accept the new operator. Each of them define a collection of predefined operations.
OclAny is an abstract type (not instanciable), ancestor of every type (except collections). Predefined operations of this type are available for everyone, including enumeration and business model classes. Note that, like OclAny, you cannot re-define operations of OclObject in the business model.
Examples:
Integer i = 0;
i.oclIsTypeOf(Real);//false
i.oclIsTypeOf(Integer);//true
i.oclIsKindOf(Real);//true
i.=(0);//true
i.<>(0);//false
i.oclAsType(Real).+(1);//the
evaluation returns a Real
OclObject is an abstract type (not instanciable), ancestor of every business classes. OclObject is a subclass of OclAny. Predefined operations of this type are available for every business model classes. Note that, like OclAny, you cannot re-define operations of OclObject in the business model.
These types are visible everywhere in the code. They are created by literal values.
Real
This is the type for mathematical real values. As told above, Real is a subclass of OclAny. Literals of type real are defined by
('0' .. '9')+
( ('.' ('0' .. '9')+)
| ( ('e' | 'E') ('+' | '-')? ('0' .. '9')+ )
| ( '.' ('0' .. '9')+ ('e' | 'E') ('+' | '-')? ('0' .. '9')+ )
)
For instance: 0.1 17.12 3.0 3e-9 3e7 3E+18 38.545e+12
Some of its main predefined operations are:
= and <>: equality and inequality
+, -, *, /: the four basic operations
floor:Integer: the integer part
abs:Real: lthe absolute part; for instance (- 12.1753e-17).abs returns 12.1753e-17
max and min: the maximum and the minimum between two real values; for instance (12.5).max(-17.3) returns 12.5
<, >, <=, >=: the four basic comparators
As Real inherits of OclAny, predefined operations of OclAny are also available as oclAsType or oclIsKindOf. A value of type Real may be retyped to OclAny.
Integer
This is the type for mathematical integer values. Integer is a kind of real, so Integer is a subclass of Real. Literals of type real are defined by
('0' .. '9')+
For instance: 1 1234 45612348 0
Some of its main predefined operations are:
+, -, *, /: the four basic operations, here between two integers; notice that the division returns a real value
div and mod: the integer division and the modulo; for instance 13.div(2) returns an integer 6 and 13.mod(2) an integer 1
min et max: the minimum and the maximum between two integers
As Integer is a subclass of Real, and Real is a subclass of OclAny, are also available operations like floor, oclAsType or oclIsKindOf. A value of type Integer may be retyped to OclAny or Real.
Boolean
This is the type for Boolean values; possible literals are true and false. Boolean is a subclass of OclAny.
Some of its main predefined operations are:
As Boolean is a subclass of OclAny, are also available operations like oclAsType or oclIsKindOf. A value of type Boolean may be retyped to OclAny.
Text / String
These are the types for character string values. Text is a subclass of OclAny, and String is a subclass of Text. Text corresponds to undefined-length strings, and String to 255-length strings. Literals are character strings between ' or ", maybe including tabulations, carriage return... For instance 'One string' or "Another string" are String / Text literals. A string may contain escape chars. These characters are introduced by the \ character:
Some of the main Text predefined operations are:
Some of the main String predefined operations are:
As Text is a subclass of OclAny, and String is a subclass of Text are also available operations like oclAsType ou oclIsKindOf. A value of type Text may be retyped to OclAny. A value of type String may be retyped to OclAny or Text.
OclType
This is the type for types. OclType is a subclass of OclAny. Its value can either be predefined types, enumeration or business model classes. Literals are given by the qualified name of the type.
Some of its main predefined operations are:
As OclType is a subclass of OclAny, are also available operations like oclAsType ou oclIsKindOf. A value of type OclType may be retyped to OclAny.
Date
This is the type for calendar dates (year / month / day). Date is a subclass of OclAny. There is no literal for this predefined type. To instanciate a date, use the static operations Date.getCurrent or Date.getDate(Integer year, Integer month, Integer day).
For instance: Date.getCurrent returns the current date; Date.getDate(2000, 7, 14) returns the July, 14th 2000.
Some of its main predefined operations are:
As Date is a subclass of OclAny, are also available operations like oclAsType ou oclIsKindOf. A value of type Date may be retyped to OclAny.
Time
This is the type for day time (hour / minute / second / millisecond). Time is a subclass of OclAny. There is no literal for this predefined type. To instanciate a time, use the static operations Time.getCurrent et Time.getTime(Integer hour, Integer minute, Integer second).
For instance: Time.getCurrent returns the current time; Time.getime(17, 0, 0) returns tea time.
Some of its main predefined operations are:
As Time is a subclass of OclAny, are also available operations like oclAsType ou oclIsKindOf. A value of type Date may be retyped to OclAny.
The Xion operation call may seem hard to use, that is why Xion define some shorthand operators. For instance, to avoid typing 1.+(1), it is possible to write 1 + 1. As other programming languages, these operators respect precedence rules. For instance 1 + 2 * 3 has not the same result as 1.+(2).*(3) but is equivalent to 1.+(2.*(3)). Here is a table that presents the operator list, their shorthand, and their priority. In case of conflict, the righter has a higher priority level (1/2*3 corresponds to 1./(2).*(3)). Notice that the operation search is made thanks to its name, whatever is its base class, even business class. So, it is possible to define a class A with an operation +(Integer):A; then you can call the operator myA + 1, or myA++ if myA is an instance of A. The only limitation comes from the fact you cannot re-define OclAny and OclObject operations.
| Operator name | Shorthand operation | Example | Equivalent example | Precedence |
| + (unary) | + | +1 | 1.+ | 1 |
| - (unary) | - | -1 | 1.- | 1 |
| ~ (unary) | ~ | ~1 | 1.~ | 1 |
| ! (unary) | not | ! true | true.not | 1 |
| * | * | 1 * 2 | 1.*(2) | 2 |
| / | / | 1 / 2 | 1./(2) | 2 |
| % | mod | 1 % 2 | 1.mod(2) | 2 |
| + | + | 1 + 2 | 1.+(2) | 3 |
| - | - | 1 - 2 | 1.-(2) | 3 |
| << | << | 1 << 2 | 1.<<(2) | 4 |
| >> | >> | 1 >> 2 | 1.>>(2) | 4 |
| < | < | 1 < 2 | 1.<(2) | 5 |
| > | > | 1 > 2 | 1.>(2) | 5 |
| <= | <= | 1 <= 2 | 1.<=(2) | 5 |
| >= | >= | 1 >= 2 | 1.>=(2) | 5 |
| instanceof | oclIsKindOf | 1 instanceof Integer | 1.oclIsKindOf(Integer) | 5 |
| == | = | 1 == 2 | 1.=(2) | 6 |
| != | <> | 1 != 2 | 1.<>(2) | 6 |
| & | & | 1 & 2 | 1.&(2) | 7 |
| ^ | ^ | 1 ^ 2 | 1.^(2) | 8 |
| | | | | 1 | 2 | 1.|(2) | 9 |
| && | and | true && false | true.and(false) | 10 |
| || | or | true || false | true.or(false) | 11 |
| implies | implies | true implies false | true.implies(false) | 12 |
Others operators are code shorthand: ++, --, +=, -=, *=, %=, <<=; >>=, &=, |=; ^=, corresponding for x and y to x = x + 1, x = x - 1, x = x + y, x = x - y, x = x * y, x = x % y, x = x << y, x = x >> y, x = x & y, x = x | y, x = x ^ y. Note that the operators ++ and --, are shorthand on X.+(Integer):X, where X is the base class; they return x for x++ and x--, x+1 for ++x, and x-1 for --x; the incrementation or decrementation is done AFTER the current expression, so op(++x, ++x); is equivalent to op(x+1, x+1); x = x + 1; x = x + 1;. These two last operations are not allowed in iterating operations. ++ and -- has a 1st precedence and assignations (as =, +=, ...) a 14th one.
The last operator is the ternary operator, that have a precedence of 13. This operator chooses to return of of two expression thanks to a Boolean one. For instance, to transform a boolean in a character string:
String bAsString = b ? "true" : "false";
Xion does not define tables but provides collection predefined types. A collection is a container, typed with a predefined type, a business class or an enumeration. This type represents the kind of contained elements. A collection cannot contain the null value, which inclusion is ignored. The most common problem is the operation access. The type name is represented by the type of the collection, post fixed with the qualified name of the element type between parenthesis. For instance Set(Real) is the collection type Set containing Real elements. Literals are represented by the type of the collection, with elements separated with a coma, between curly brackets. For instance, Bag{1,2,3,4}, whose type is named Bag(Byte), is a Bag containing the Byte values 1, 2, 3 and 4. The operator .. allows a range between Integers, for instance Bag{1..4}. The elements may be given as expression instead of literals (as Bag{x*3 .. x*3+18}). Remarking Byte inherits of Real, Bag(Byte) is equivalent to Bag(Real), but not of Bag(String). Remarking Bag is a subclass of Collection, Bag(Byte) conforms to Collection(Byte), and Collection(Real), but not to Collection(String).
Operation access
Accessing predefined operations on collections is a bit different from other operations. The indirection is not represented by the character . but the character sequence ->. The character . is here used as a shorthand for the collect predefined operation.
Examples:
Collection
OclObject is an abstract type (not instanciable), ancestor of every concrete collection types. It does not inherit of OclAny. In that each collection type is a subtype of Collection, and every non-collection type is a subclass of OclAny, every collection conforms to Collection(OclAny).
Some of its main predefined operations are:
Moreover, exist some operations said "iterating operations", that will evaluate an expression, given as a parameter, iterating over each element of the collection. For instance, the isUnique operation determines if the expression given as parameter evaluates to different results for each element of the collection.
For a Collection(String) containing "a", "ab", "abc", the operation isUnique(size) will return true. If this collection would have contained "ba", the result would have been false. In fact, size, evaluated over each element of the collection, has returned 1, 2 and 3: isUnique has determined that 1 != 2, 1 != 3 and 2 != 3. If the collection had contained "ba", the return set of size would have been 1, 2, 3 and 2: 2 == 2 so the result is false. See more detailed iterating operations for better explanations.
Set
This is the type for the mathematical set, that is it cannot contain more than one occurrence of the same element. The operation = is used here to determine the comparison. Set is a collection, a subclass of Collection. There is no order in a Set.
The literal for Set is Set { <a value>, <another value>, ...}. Values may be expressed by Xion expressions, as literals. For Set of Integer (or each subclass of Integer as Long, Int,...), it is possible to specify an interval: Set { <an integer> .. <a greater integer>}. The empty Set is given by Set {}; this is the only way to build a Set(Void); you may have to cast it in very specific cases, but this type conforms to other Set and Collection.
For a Set of Integers (named Set(Integer)), Integer inheriting of Real and Real inheriting of OclAny, a Set(Integer) conforms to Set(Real), to Set(OclAny), to Collection(Integer), to Collection(Real) and to Collection(OclAny).
Some of its main predefined operations are:
As Set is a subclass of Collection, are also available operations from Collection.
Bag
This is the type for container where elements can appear more than once. Bag is a collection, a subclass of Collection. There is no order in a Bag.
The literal for Bag is Bag { <a value>, <another value>, ...}. Values may be expressed by Xion expressions, as literals. For Bag of Integer (or each subclass of Integer as Long, Int,...), it is possible to specify an interval: Bag { <an integer> .. <a greater integer>}. The empty Bag is given by Bag {}; this is the only way to build a Bag(Void); you may have to cast it in very specific cases, but this type conforms to other Bag and Collection.
For a Bag of Integers (named Set(Integer)), Integer inheriting of Real and Real inheriting of OclAny, a Bag(Integer) conforms to Bag(Real), to Bag(OclAny), to Collection(Integer), to Collection(Real) and to Collection(OclAny).
Some of its main predefined operations are:
As Bag is a subclass of Collection, are also available operations from Collection.
Sequence
This is the type for a container where elements are ordered. An element may appear more than once in a Sequence. The first element has an index value of 0 . Sequence is a collection, a subclass of Collection.
The literal for Sequence is Sequence { <a value>, <another value>, ...}. Values may be expressed by Xion expressions, as literals. For Sequence of Integer (or each subclass of Integer as Long, Int,...), it is possible to specify an interval: Sequence { <an integer> .. <a greater integer>}. The empty Sequence is given by Sequence {}; this is the only way to build a Sequence(Void); you may have to cast it in very specific cases, but this type conforms to other Sequence and Collection.
For a Sequence of Integers (named Set(Integer)), Integer inheriting of Real and Real inheriting of OclAny, a Sequence(Integer) conforms to Sequence(Real), to Sequence(OclAny), to Collection(Integer), to Collection(Real) and to Collection(OclAny).
Some of its main predefined operations are:
As Sequence is a subclass of Collection, are also available operations from Collection.
exists and forAll
exists and forAll are iterating operations defined in the predefined class Collection. These operations have an expression as parameter that will be applied to each element of the collection. For exists and forAll this expression must return a Boolean value. exists checks that this expression returns true at least once, and forAll checks that this expression returns true for each occurence.
Examples:
For Car, a business call defining the public attribute color with type the enumeration Color. This enumeration defines the enumerated red. For parking a collection of Car.
Is there a red car on the parking: parking->exists(color == # red)
Are every car on the parking red: parking->forAll(color == # rouge)
Remarks:
The normal order of feature searching is variable - type - attribute - link - operation. In an iterating operation, this order is attribute - link - operation - variable - type, attribute - link - operation being firstly searched into the current element of the collection. To retrieve a context, you may have to use the this / self variable.
It is also possible to name the current element as : parking->exists(theCurrentCar: theCurrentCar.color == # red). The, the feature searching order is variable - type - attribute - link - operation. This is the only way to access an above defined variable color.
select et reject
select and reject are iterating operations defined in Set, Bag and Sequence. These operations have an expression as parameter that will be applied to each element of the collection. For select and reject this expression must return a Boolean value. select will build a new collection rejecting the elements for which the expression returns false. reject will build a new collection rejecting the elements for which the expression returns true
Exmples:
For Car, a business call defining the public attribute color with type the enumeration Color. This enumeration defines the enumerated red. For parking a collection of Car.
The red cars on the parking: parking->select(color == # red) or parking->reject(color != # red)
The non-red cars on the parking: parking->reject(color == # red) or parking->select(color != # red)
Remarks:
The normal order of feature searching is variable - type - attribute - link - operation. In an iterating operation, this order is attribute - link - operation - variable - type, attribute - link - operation being firstly searched into the current element of the collection. To retrieve a context, you may have to use the this / self variable.
It is also possible to name the current element as : parking->select(theCurrentCar: theCurrentCar.color == # red). The, the feature searching order is variable - type - attribute - link - operation. This is the only way to access an above defined variable color.
collect
collect is an iterating operation defined in Set, Bag and Sequence. This operation has an expression as parameter that will be applied to each element of the collection. collect build a Bag (or a Sequence if applied on a Sequence) containing the result of the expression applied to each element of the collection. As told previously, there is a shorthand that consists of replacing ->collect by ..
Example:
For Car, a business call defining the public attribute color with type the enumeration Color. This enumeration defines the enumerated red. For parking a collection of Car.
The color list of the car on the parking: parking->collect(color) or parking.color
To eliminate duplicates: parking.color->asSet
Remarks:
The normal order of feature searching is variable - type - attribute - link - operation. In an iterating operation, this order is attribute - link - operation - variable - type, attribute - link - operation being firstly searched into the current element of the collection. To retrieve a context, you may have to use the this / self variable.
It is also possible to name the current element as : parking->collect(theCurrentCar: theCurrentCar.color). The, the feature searching order is variable - type - attribute - link - operation. This is the only way to access an above defined variable color.
Enumeration types are defined in the business model. An enumeration literal (also called enumered) is pre-fixed by the # character. You can refer examples given in the definitions of select, exists or collect. As enumeration are subtypes of OclAny, are available predefined operations of OclAny like oclAsType or oclIsKindOf. Moreover is defined the toString operation that returns the name of the enumeration literal as a String.
Integer and Real are generic types, and their coding format depends on the target database where objects are stored for persistency and sharing. To store the maximum number of values, attributes of type Real and Integer are stored in the largest format that the database provides. That is why, to limit the database size, to solve performance of stocking problem, were added specific integer and real types, that define the stocking format.
Byte is defined on 8 bits, Short on 16, Int on 32 and Long on 64. Integer types define binary operations such as and, inclusive or, exclusive or, shift left and shift right. Moreover, predefined operations are overridden in subclasses to limit values inflation during operations; for instance calling +. Conformance is given by the paragraph Types relations.
Float is defined on 32 bits and Double no 64. Predefined operations are overridden to limit values inflation during operations; for instance calling +. Conformance is given by the paragraph Types relations.